Equipartition and Mass Segregation
Simulations of star clusters with two mass components
Abstract
The dynamical evolution of an isolated self-gravitating system
is studied under the aspects of mass segregation and equipartition
processes.
We analyse the idealized case of a cluster with two distinct mass
components.
The individual ratio of the heavy to light bodies, \mu = m_2/m_1,
is varied from 1.25 to 50.0 and the fraction of the total heavy
mass q is altered from 5% to 40% of the whole cluster.
We also examine the cluster properties like the core collapse,
the evolution of the central potential, the radial stratification
of masses as well as escapers.
We present new, high-accuracy collisional N-body simulations,
using the high-order integrator NBODY6++.
We modelled up to N = 20,000 particles on the parallel
supercomputer CRAY T3E, and the statistical significancy of the
lower-N simulations was improved by ensemble averages.
Our objective is to check the various theories on early star
formation and dynamical evolution.
We find significant deviations of the evolutionary time scale in
the regime \mu —> 1.
Equipartition slows down the gravothermal contraction of the core
slightly.
Beyond a critical value of \mu ~ 2, no equipartition can be
achieved between the different masses, a phenomenon known as the
Spitzer equipartition instability; the heavy component decouples
and collapses under the influence of the gravothermal instability
of its own subsystem.
For the first time the critical boundary between Spitzer-stable
and -unstable systems is demonstrated in direct N-body models.
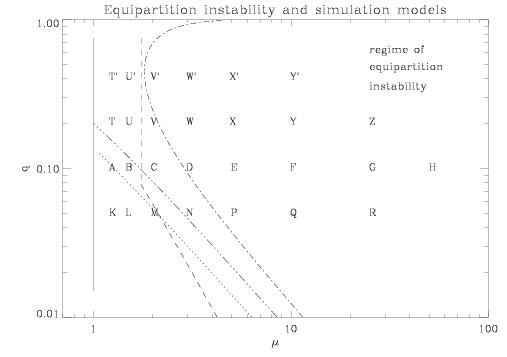
Parameter space of the models examined in this work.
The position of the Roman letters indicate a model determined
by its q and mu.
The lines are the borders for equipartition stability as
proposed by various theories (Fig. 8.1).
Last modified: 2015, Apr 18







